Rational Number – Its Decimal Representation

Decimal Representation of Rational Numbers are broadly classified into 2(two) groups:
- Terminating Decimal Representation
- Non-Terminating, Repeating Decimal Representation
Any Rational Number can be expressed in Decimal Form either as Terminating DR or Non-Terminating, Repeating DR.
Let us understand this concept with a suitable example.
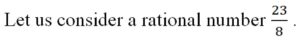
In order to know its DR, we have to divide 23 by 8 that is 23 ÷ 8.
(For better understanding, we can write 23 as 23.000) 
On Dividing 23 by 8, the reminder terminates that is the reminder becomes 0(zero).
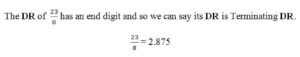
In general we can say that, a Rational Number has its Terminating DR if and only if, it has an end digit.
Rational Number – Its Decimal Representation (Continued……………….)
Again, Let us consider a rational number
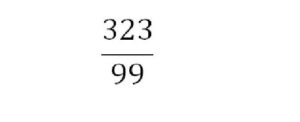
In order to know its DR, we have to divide 323 by 99 that is 323 ÷ 99 (For better understanding, we can write 323 as 323.000000)

On Dividing 323 by 99, we see that the decimal parts continue endlessly with number of groups of digits repeated again & again and so we can say its DR is Non-Terminating, Repeating DR.
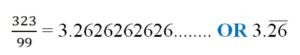
Complementary Angles, Supplementary Angles & Linear Pair Axiom and its Converse
In general, we can say that a Rational Number has its Non-Terminating, Repeating Decimal Representati0n if and only if its decimal parts continue endlessly with number of groups of digits repeated again & again.
Application of Rational Numbers:
One can observe or realize the application of rational numbers in their day to day life:-
1) For calculation of Tax Calculation in the form of fractions.
2) Calculation of Interest rates on loans and mortgages, Savings Account and so on.
3) Homework not completed by students. In such a case, response comes as half portion or 50% etc completed.
4) During share of a pizza or anything with someone.





