Properties of Rational Numbers

1. Additive Properties (Properties due to Addition): Properties of Rational Numbers

                      a) Closure Property of Addition: The Set of Rational Numbers is closed with respect to the operation of Addition. In general, it means that the sum of Rational Numbers is always a Rational Number.

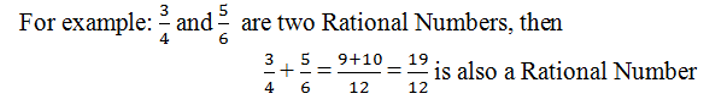
              b) Commutative Law of Addition: If a and b are two Rational Numbers, then

                                                       a + b = b + a.

This is know as Commutative Law of Addition in the Set of Rational Numbers.

 

       c) Associative Law of Addition: If a, b and c are three Rational Numbers, then

                                        a + (b + c) = (a + b) + c

This is know as the Associative Law of Addition in the Set of Rational Number.

         d) Existence of Additive Identity: For every Rational Number a, there exist a unique Rational Number 0 (Zero) such that

                                                                     0 + a = a + 0 = a

                                0 (Zero) is called the Additive Identity in the Set of Rational Numbers          

           

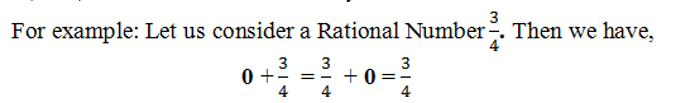
       e) Existence of Additive Inverse: For every Rational Numbers a, there exist a unique Rational Number –a such that

                                                                a + (–a) = –a + a = 0

                                a is called the Additive Inverse of –a and vice-versa in the Set of Rational Numbers                

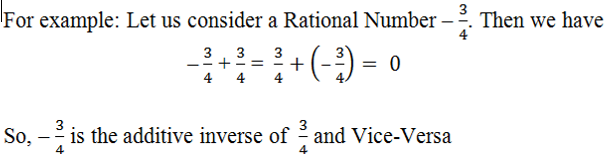
 2. Multiplicative Properties (Properties due to Multiplications):

      a) Closure Property of Multiplication: The Set of Rational Numbers is closed with respect to the operation

of Multiplication. In general, it means that the Product of Rational Numbers is always a Rational Number.

This is know as the Close Property of Multiplication in the Set of Rational Numbers.

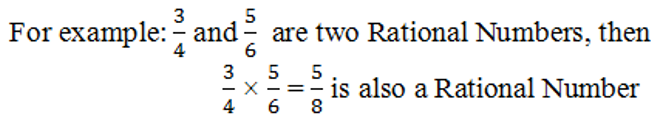
     b) Commutative Law of Multiplication: If a and b are two Rational Numbers, then

                                               a × b = b × a.

This is know as the Commutative Law of Multiplication in the Set of Rational Numbers

     c) Associative Law of Multiplication: If a, b and c are three Rational Numbers, then

                                         a × (b × c) = (a × b) × c

This is know as the Associative Law of Multiplication in the Set of Rational Numbers.

      d)  Existence of Multiplicative Identity: For every Rational Number a, there exist a unique Rational Number 1 (one) such that

                                         a × 1 = 1 × a = a

1 (one) is call the Multiplicative Identity in the Set of Rational Numbers

Fast Fact:-

  (i) The Set of Rational Numbers is close with respect to the operation of Subtraction. The Difference of two Rational numbers is always a Rational Number.

Illustrate yourself with suitable example.

  (ii)The Set of Rational Numbers is close with respect to the operation of Division. The Quotient of two Rational Numbers is always a Rational Number.

Illustrate yourself with suitable example.

  (iii) All Natural Numbers, Whole Number and Integers are Rational Numbers. Illustrate yourself with suitable example.

Factors and Multiples -Factors, Common Factors, Highest Common Factors (H.C.F.)

Enquiry related to SBI Balance Enquiry and Mini Statement of SBI Account