Quadratic Polynomial, Quadratic Equation and Solution of Quadratic Equation

Quadratic Equation class 10

Quadratic Polynomial, Quadratic Equation and Solution of Quadratic Equation

(Discriminant of Quadratic Equation and Relation between Roots of the Quadratic Equation)

The Standard form or General Form of Quadratic Polynomial is ax² + bx + c, where a, b and c are constants and x is the variable.

The Standard Form or General Form of Quadratic Equation is

ax² + bx + c = 0

where a, b and c are constants and x is the variable.

The values of x which satisfies the Quadratic Equation are called its solutions or roots. A Quadratic Equation has two distinct roots or two equal roots. The roots of the equations may be Real Roots representing real numbers as well as Imaginary Roots representing Complex Numbers.

Derivation of Roots of Quadratic Equation

Sum and Products of roots of Quadratic Equation

The roots of the Quadratic Equation are ax² + bx + c = 0 are

Now, sum of roots is

 

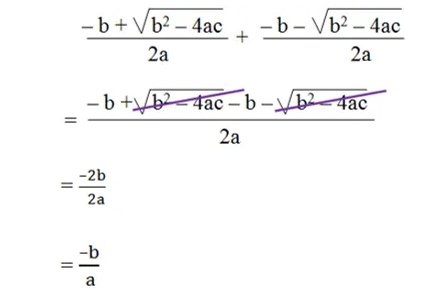
Quadratic equation class 10:- Hence the sum of the roots of the quadratic equation ax² + bx + c = 0 is

Again, the roots of the Quadratic Equation are ax² + bx + c = 0 are

Basic Proportionality Theorem or Thales Theorem

Now, Product of roots is

Hence the products of the roots of the quadratic equation ax² + bx + c = 0

Once again, we have, the Standard Form or General Form of Quadratic Equation is

ax² + bx + c = 0

Dividing both sides by a, we get

The Quantity b² – 4ac is called the Discriminant of the Quadratic Equation ax² + bx + c = 0 and it is denoted by D.

D = b² – 4ac

1. If Discriminant D ≥ 0, then the Quadratic Equation has two real roots.

(I) If Discriminant D > 0, the Quadratic Equation has two Distinct Real Roots.

(II) If Discriminant D = 0, the Quadratic Equation has two Equal Real Roots.

Math Quadratic equation class 10

 

2. If Discriminant D < 0, the Quadratic Equation has NO Real Roots. It has Imaginary Roots representing Complex Numbers.

National Mathematics Day of India –राष्ट्रीय गणित दिवस