Trigonometric Identities and its Derivation

Trigonometric Identities (TI) and its Derivation

Trigonometric identities: A brief description on Trigonometry and Trigonometric Ratios has been provided on the website link Trigonometric Ratios.

Now, let us know about TI and its Derivation.

Basically, there are 3(three) Trigonometric identities viz.,

  1. cos2θ + sin2θ = 1
  2. 1+ tan2θ = sec2θ
  3. 1 + cot2θ = cosec2θ

In order to derive these three Trigonometric Identities, let us consider a Right-angled triangle, △ABC right angled at A that is ∠BAC = 90°

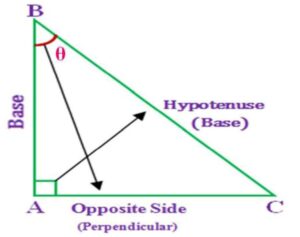
Trigonometric Ratios

According to Pythagoras Theorem, we know that in a Right-angled triangle, the sum of the square of the Hypotenuse (Longest Side of the right-angled triangle) is equal to the sum of the squares of the other two sides.

(Perpendicular)2 = (Perpendicular)2 + (Base)2

Triogonometric Identities

Trigonometric Identities

Trigonometric Identities

Hence, 3(three) Derived Trigonometric Identities, mentioned above are:

1)      cos2θ + sin2θ = 1

2)      1+ tan2θ = sec2θ

3)   1 + cot2θ = cosec2θ

 

From 1), we have

(a) cos2θ = 1 – sin2θ

(b) sin2θ = 1 – cos2θ

From 2), we have

(a) sec2θ – tan2θ = 1

(b) tan2θ = sec2θ – 1

 

From 3), we have

(a) cosec2θ – cot2θ = 1

(b) cot2θ = cosec2θ – 1

Hipparchus of Nicaea

Hipparchus of Nicaea (190 BC – 120 BC) , a Greek astronomer, geographer, and mathematician is considered as the founder of trigonometry but is most famous for his incidental discovery of Precession of the Equinoxes.
The application of Spherical Trigonometry is seen in Astronomy which deals with the study of Heavenly Bodies like planets, stars, galaxies, etc, its position and distances between various heavenly bodies of the universe.
Post Views: 1,186

2 thoughts on “Trigonometric Identities and its Derivation”

  1. Pingback: Trigonometric Ratios of Complementary Angles - School Academy
  2. Pingback: Classification Matrix - CLASSIFICATION OF MATRICES

Leave a Comment