Trigonometry (Trigonometric Ratios – Measurement of Triangles)
The word Trigonometry is a 16th Century Latin Derivative from the Greek Words viz., TRIGONON which means Triangle and METRON which means Measurement.
So, the measurement of triangle in respect of its angles, sides, perimeter and area is known as Trigonometry.
The measurement of triangle can be done by the application of Trigonometric Ratio.
Trigonometric Ratios are the ratio of any two sides of a Right-Angled Triangle.
Let us understand the details of Trigonometric Ratios mentioned as under.
Let us consider a Right-angled triangle, △ABC right angled at A that is ∠BAC = 90°

Other than ∠BAC = 90°, let us consider another angle, say ∠B or ∠ABC or ∠CBA = θ
Now,
Side opposite to θ is AC. This side is called Opposite Side or Perpendicular Side of △ABC
Side opposite to Right Angle (90°) is BC. This side is called Hypotenuse and it is the longest side of a Right-Angled Triangle
The remaining third side of △ABC is AB. This side is called the Base of the △ABC.
Considering any two sides of the Triangle and taking their ratio, we will get 6(Six) Trigonometric Ratios, which are-
(i) sine of the angle (abbreviated as sin θ)
(ii) cosine of the angle (abbreviated as cos θ)
(iii) tangent of the angle (abbreviated as tan θ)
(iv) cotangent of the angle (abbreviated as cot θ)
(v) secant of the angle (abbreviated as sec θ)
(vi) cosecant of the angle (abbreviated as cosec θ)
The description of all these 6(six) trigonometric angles are:

Relationship among the Trigonometric Ratios:
From the above expression, one can easily state that the Reciprocal Relation or Multiplicative Inverse relation exist in between the pairs of specified Trigonometric Ratios. These reciprocal relations or Multiplicative Inverse Relation of specified Trigonometric Ratios are:
sin θ and cosec θ are reciprocal or multiplicative inverse of each other, so we can write as

As we know that the product of a number and its reciprocal is 1, so the reciprocal or multiplicative inverse relation specified Trigonometric Ratio can also be written as

Similarly, we have

&

Fast Fact to know:
It is known from algebra that variable are denoted by generally small letters of the English Alphabets like x, y, z, p, q, r and so on.
Similarly, angles are denoted by

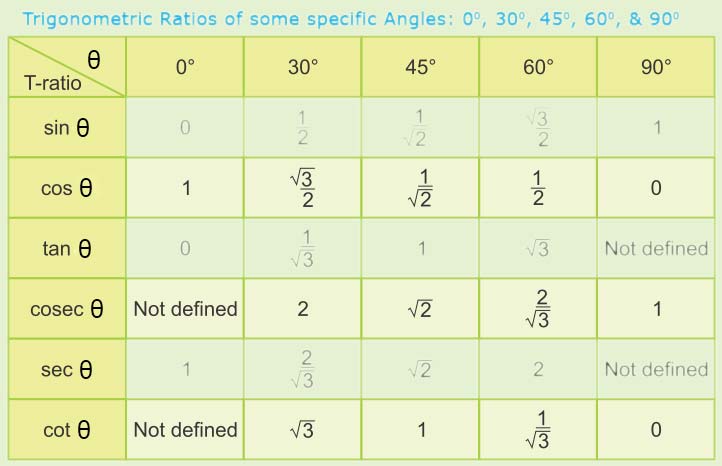
It is very easy to remember all the trigonometric ratios. Commit to memory the sentence

Rational Number – Its Decimal Representation





4 thoughts on “Trigonometric Ratios”