find the center and radius of the circle

Find the Center and Radius of the Circle

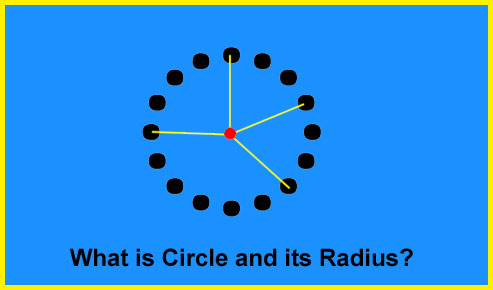
What is Circle and its Radius?

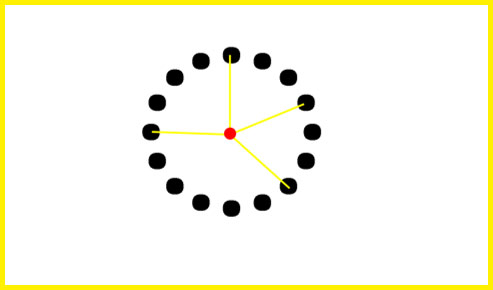
In the above figure, we observe that

1. Black Dots represent the set of all those Points which are located at a FIXED Distance from the FIXED Red Point.
2. The distances between the FIXED Red Point and set of all those Black Points is fixed. It is actually the length of Yellow Coloured Line Segment joining the FIXED Red Point and any Black Point.

From the above observations, we conclude that

1. The set of all those points which are located at a fixed distance from a fixed point is known as Circle.
2. The fixed point is called the CENTRE of the Circle and the fixed distance is called the RADIUS of the circle.

How can we denote a Circle?

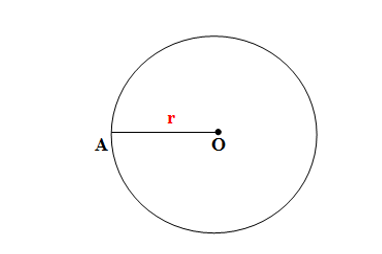
A is a point on the Circle and O is the Centre of the circle. So, AO = r is the length of the radius of the Circle

A Circle with Centre O and radius r is denot by

                                                                                                                                                           C(O,r)

Find the Center and Radius of the Circle – Chord and Diameter of a Circle

We have,

M and N are two points on the Circle C(O,r). So, the line segment MN is formed by joining the two points M and N on the Circle.

Secondly, P and Q are also other two points on Circle C(O,r). The line segment PQ is form by joining the two points P and Q on the Circle and it also passes through the centre O of the Circle.

The line segment form by joining any two points on the Circle is call its CHORD. In the above figure, MN is the Chord of the Circle.

The line segment form by joining any two points on the Circle and pass through the centre of the Circle is call its DIAMETER. In the above figure PQ is the Diameter of the Circle.

“The Diameter is the longest of the Circle”

 Relation between RADIUS and DIAMETER of Circle

It is find that the length of the Radius of a Circle is HALF the length of the diameter

OR

The length of the Diameter of a Circle is TWICE the length of its Radius.

If r is the length of the Radius of the Circle and d is the length of its Diameter, then the mathematical relationship between them can be express as

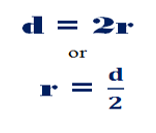
Circumference and Area of Circle

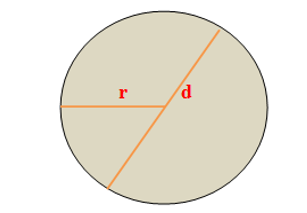
The entire shaded portion of the Circle is the Area of the Circle.

If a rope or thread is use to make a Circle, then the total length of it is call the CIRCUMFERENCE or PERIMETER of the Circle.

If r and d are the Radius and Diameter of the Circle respectively, then the mathematical expression for Circumference and Area of the Circle can be express as-

Circumference of a Circle

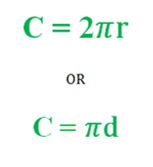
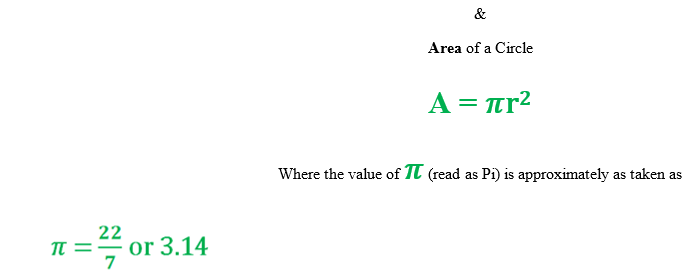
Basic Proportionality Theorem or Thales Theorem

SBI EMI Calculator | Equated Monthly Installments – EMI