Rectilinear Figures
(Quadrilateral)
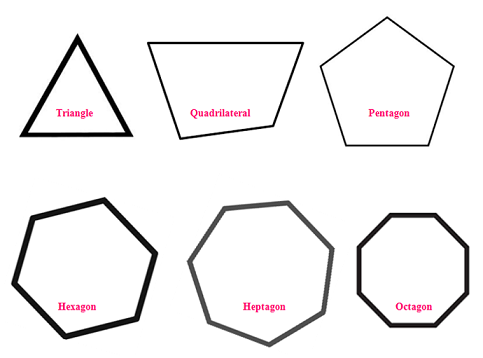
A closed geometrical figure bounded by Straight lines is called Rectilinear Figures. There are various forms of Rectilinear Figures:
- Triangle – Rectilinear Figures with 3 sides
- Quadrilateral – Rectilinear Figures with 4 sides
- Pentagon – Rectilinear Figures with 5 sides
- Hexagon – Rectilinear Figures with 6 sides
- Heptagon – Rectilinear Figures with 7 sides
- Octagon – Rectilinear Figures with 8 sides
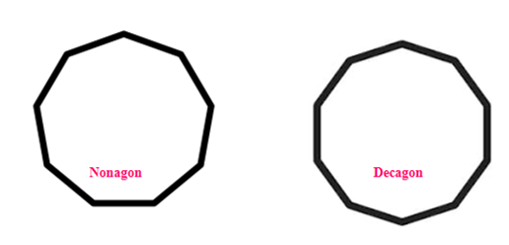
- Nonagon – Rectilinear Figures with 9 sides
- Decagon – Rectilinear Figures with 10 sides and so on
Quadrilateral
A rectilinear figure having 4(four) sides is called Quadrilateral.
In general, a Quadrilateral has
- 4(Four) Sides
- 4(Four) Angles
- 2(Two) Diagonals
- 4(Four) Vertices
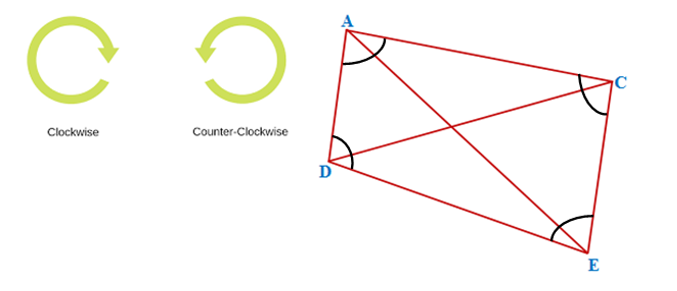
The above figure represents a Quadrilateral whose name can be written in various ways by arranging the capital letters of the English Alphabets A, B, C and D either in Clockwise Direction or Anti-Clockwise Direction.
Accordingly, the various names of above Quadrilateral Figures are
- ▭ ACED or Quad. ACED (Clockwise arrangement of Alphabets)
- ▭ DACE or Quad. DACE (—————-do—————-)
- ▭ ADEC or Quad. ADEC (Anticlockwise arrangement of Alphabets)
- ▭ ECAD or Quad. ECAD (—————-do—————-)
The 4(Four) sides of ▭ ACED or Quad. ACED are
- AC or CA
- CE or EC
- ED and DE
- AD or DA
The 4(Four) Angles of ▭ ACED or Quad. ACED are
- ∠DAC or ∠CAD
- ∠ACE or ∠ECA
- ∠CED or ∠DEC
- ∠ADE or ∠EDA
The 2(Two) diagonals of ▭ ACED or Quad. ACED are
- AE or EA
- CD or DC
The 4(Four) Vertices of ▭ ACED or Quad. ACED are Point A, Point C, Point E and Point D.
Types of Quadrilateral
Various types of Quadrilateral are:
- Square
- Rectangle
- Rhombus
- Parallelogram
- Trapezium
- Kite
Square

A Square is a Quadrilateral in which
(a) All Sides are equal
(AB = BC = CD = AD)
(b) All Angles are equal, each of measure 90°
∠BAD = ∠ABC = ∠BCD = ∠ADC = 90°
(c) The Diagonal are equal and bisect each other at right angle
The Diagonal AC bisects diagonal BD at right angle. It means that the diagonal AC divides the diagonal BD into two equal parts making an angle of measure 90°.at the point of intersection of diagonals.
Similarly, The Diagonal BD bisects diagonal AC at right angle. It means that the diagonal BD divides the diagonal AC into two equal parts making an angle of measure 90°.at the point of intersection of diagonals.
(d) Both Pairs of Opposite Sides are Parallel
AB ∥ CD and BC ∥ AD
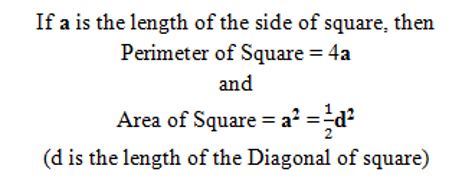
Rectangle
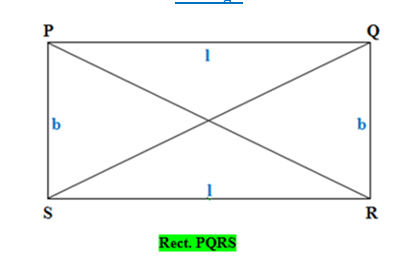
A Rectangle is a Quadrilateral in which
(a) Pairs of Opposite Sides are equal and parallel. Adjacent Sides are Unequal. The longer side is called the length of the Rectangle and shorter side is called the breadth of the rectangle.
(PQ = SR, PQ ∥ SR and QR = PS, QR ∥ PS)
(b) All Angles are equal, each of measure 90°
∠SPQ = ∠PQR = ∠QRS = ∠RSP = 90°
(c) The Diagonal are equal and bisect each other at any angular measurement.
The Diagonal PR bisects diagonal SQ. It means that the diagonal PR divides the diagonal SQ into two equal parts.
Similarly, The Diagonal SQ bisects diagonal PR. It means that the diagonal SQ divides the diagonal PR into two equal parts.
If l is the length and b is the breadth of the rectangle, then
Perimeter of Rectangle = 2(l + b)
and
Area of Rectangle = l × b
Rhombus
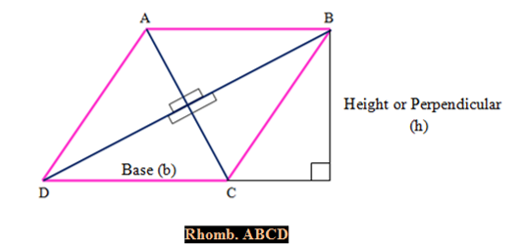
A Rhombus is a Quadrilateral in which
(a) All Sides are equal
(AB = BC = CD = AD)
(b) All Angles are not equal, but opposite angles are equal
∠BAD = ∠BCD and ∠ABC = ∠ADC.
(c) The Diagonal are not equal, but bisect each other at right angle
The Diagonal AC bisects diagonal BD at right angle. It means that the diagonal AC divides the diagonal BD into two equal parts making an angle of measure 90°.at the point of intersection of diagonals.
Similarly, The Diagonal BD bisects diagonal AC at right angle. It means that the diagonal BD divides the diagonal AC into two equal parts making an angle of measure 90°.at the point of intersection of diagonals.
(d) Both Pairs of Opposite Sides are Parallel
AB ∥ CD and BC ∥ AD
If b is the side, h is the height, d1 and d2 are the diagonals of Rhombus then
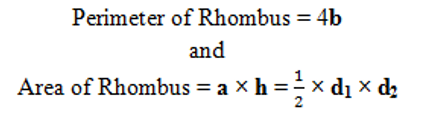
A Parallelogram is a Quadrilateral in which
(a) Pairs of Opposite Sides are equal and parallel. Adjacent Sides are Unequal.
(AB = CD, AB ∥ CD and BC = AD, BC ∥ AD)
(b( All Angles are not equal, but Opposite angles are equal
∠BAD = ∠BCD and ∠ABC = ∠ADC
(c) The Diagonal are not equal, but bisect each other at any angular measurement.
The Diagonal AC bisects diagonal BD. It means that the diagonal AC divides the diagonal
BD into two equal parts.Similarly, The Diagonal BD bisects diagonal AC.
It means that the diagonal BD divides the diagonal AC into two equal parts.
If b is the base and h is the height of the Parallelogram, then
Perimeter of Rectangle = Sum of all sides of Parallelogram
and
Area of Parallelogram = b × h
Trapezium
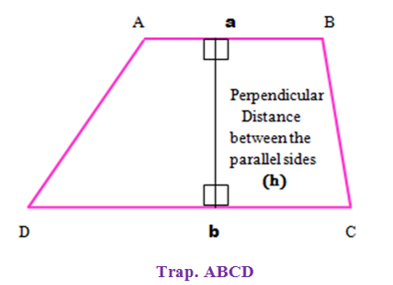
A Trapezium (also known as Trapezoid) is a Quadrilateral in which
One Pair of Opposite Sides are parallel.
(AB ∥ CD)
Do you Know Banking Awareness?
If a and b are the length of the parallel sides of the Trapezium & h is the perpendicular distance between them, then
A Trapezium in which non-parallel sides are of equal length is known as Isosceles
Trapezium otherwise they are said to be Scalene Triangle.

▭ ABCD is a Isosceles Trapezium with Side AD = Side BC
(In Isosceles Triangle the Diagonals are equal and in Scalene Trapezium, the Diagonal are not equal.)
Kite
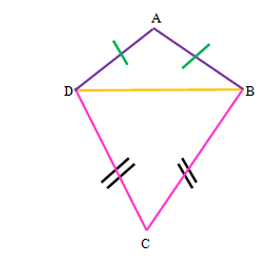
A Kite is a Quadrilateral in which both pairs of Adjacent Sides are equal. In other words,
we can say that a Kite is made up of two Isosceles Triangles having common Base.
(AD = AB & CD = CB, BD is the common Base of Isosceles Triangles viz., △ADB & △CDB)
- find the center and radius of the circle
-
What are parallel lines? | Properties of Transversal of Parallel Lines




