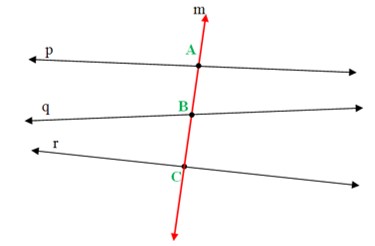
Parallel lines and transversal: If a line intersects two or more lines in a plane then it is called the transversal of the given lines.

In the figure given above, there are three lines viz., line p, line q and line r lying on a plane and the red coloured line m intersect or touch the three given lines at three distinct points A, B and C. So, line m is the transversal of the line p, line q and line r.
If a line intersect two lines lying on a plane, then 8(eight) angles are formed OR It can also be stated as if a transversal intersect 2(two) lines then 8(eight) angles are formed

The 8(eight) angles formed in the above figure are categorized into following pairs mentioned as under:
- Vertically Opposite Angles:
4(Four) pairs of Vertically Opposite Angles formed by a transversal of two lines are:-
- ∠1 and ∠4
- ∠2 and ∠3
- ∠5 and ∠8
- ∠6 and ∠7
- Corresponding Angles
4(Four) pairs of Corresponding Angles formed by a transversal of two lines are:-
- ∠1 and ∠6
- ∠2 and ∠5
- ∠3 and ∠8
- ∠4 and ∠7
- Alternate Interior Angles
2(Two) pairs of Alternate Interior Angles formed by a transversal of two lines are:-
- ∠3 and ∠5
- ∠6 and ∠4
- Alternate Exterior Angles
2(Two) pairs of Alternate Exterior angles formed by a transversal of two lines are:-
- ∠1 and ∠7
- ∠2 and ∠8
Parallel lines
When two or more lines on a plane do not meet each other then they are called Parallel Lines otherwise they are said to be Intersecting lines

Parallel lines and transversal
In the above figure, we see that although the three lines viz., line m, line n and line p extend endlessly in their both direction, but they never meet or intersect with each anywhere or at any point on the plane. Hence, we can say that these three lines are parallel to each other. Symbolically, the parallelism of these three lines can be written as
line m ∥ line n (read as line m is parallel to line n)
line m ∥ line p (read as line m is parallel to line p)
line n ∥ line p (read as line n is parallel to line p)

These three lines are Intersecting lines because it is clear cut observation from the figure that the lines meet or intersect with each other at particular point or points.

These two lines on further extension seem to meet or intersect each other at a point and so they are intersecting lines.
Note to remember:
- The symbol of parallelism of two lines is denoted by ∥ and read as “is parallel to”
- Two lines Parallel to a same given line are parallel to each other.

then from (i) and (ii), we get

3. If line m is parallel to line q, the we can write in either of the symbolic form as






1 thought on “Transversal of a Line”