Adjacent Angles

Adjacent Angles

Adjacent Angles-

Two angles are said to be adjacent angle if and only if

1. They have a common vertex
2. They have a common arm
3. Non-Common Arms are the opposite sides of the common arm

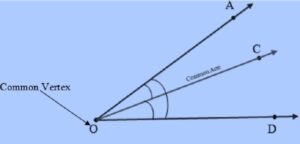
In this figure, there are three angles viz., ∠AOC or ∠COA, ∠COD or ∠DOC and ∠AOD or ∠DOA, among which ∠AOC or ∠COA and ∠COD or ∠DOC have

1. A common vertex named as point O
2. A common arm named as Ray OC
3. Non- Common arms viz., Ray OA and Ray OD are on the opposite side of Common Arm named as Ray OC.

Angle and its classification | angle classification geometry

Hence, ∠AOC or ∠COA and ∠COD or ∠DOC are Adjacent Angles.

From the figure, we have one more observations.

Point C is in the interior of ∠AOD or ∠DOA and accordingly, we have

Thus, Angle Addition Axiom States that the measure of an angle formed by two adjacent angle is equal to the sum of the measure of that two adjacent angle.

Point of Intersection and Vertically Opposite Angles

The point of Intersection of two or more lines is the point where they pass through or cross each other at a particular common point.

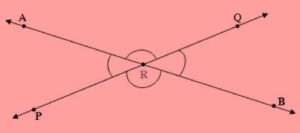
In this figure, we see that Line AB and Line PQ pass through or cross each other at a particular common point R and accordingly we can say that that Line AB and Line PQ intersect each other at a Point R

Point R is the point of intersection of two lines AB and PQ.

Now, again from the figure we have one more observation. When two lines AB and PQ cross each other at a particular common point R, then four angles are formed among which the angle opposite to each other are refer to as Vertically Opposite Angles. Two pairs of vertically opposite angle formed are:

1. ∠ARQ and ∠BRP

2. ∠PRA and ∠BRQ

 Thus “The Pairs of opposite angles formed by the Intersection of two lines are Vertically Opposite Angles”.

Pairs of Vertically Opposite Angle are always equal.

∠ARQ = ∠BRP and ∠PRA = ∠BRQ

• Three Reasons Why the Veto Power is So Important
• नाटो क्या है? What is Nato?
• UP TET News Today | यूपी टेट को लेकर बड़ी खबर
• Saarthi app SEBI (Securities and Exchange Board of India)
• Bappi Lahiri Age | Bappi Lahiri We Lost A great singer